MCQ College Board 3
Blog about the collegeboard MCQ
-
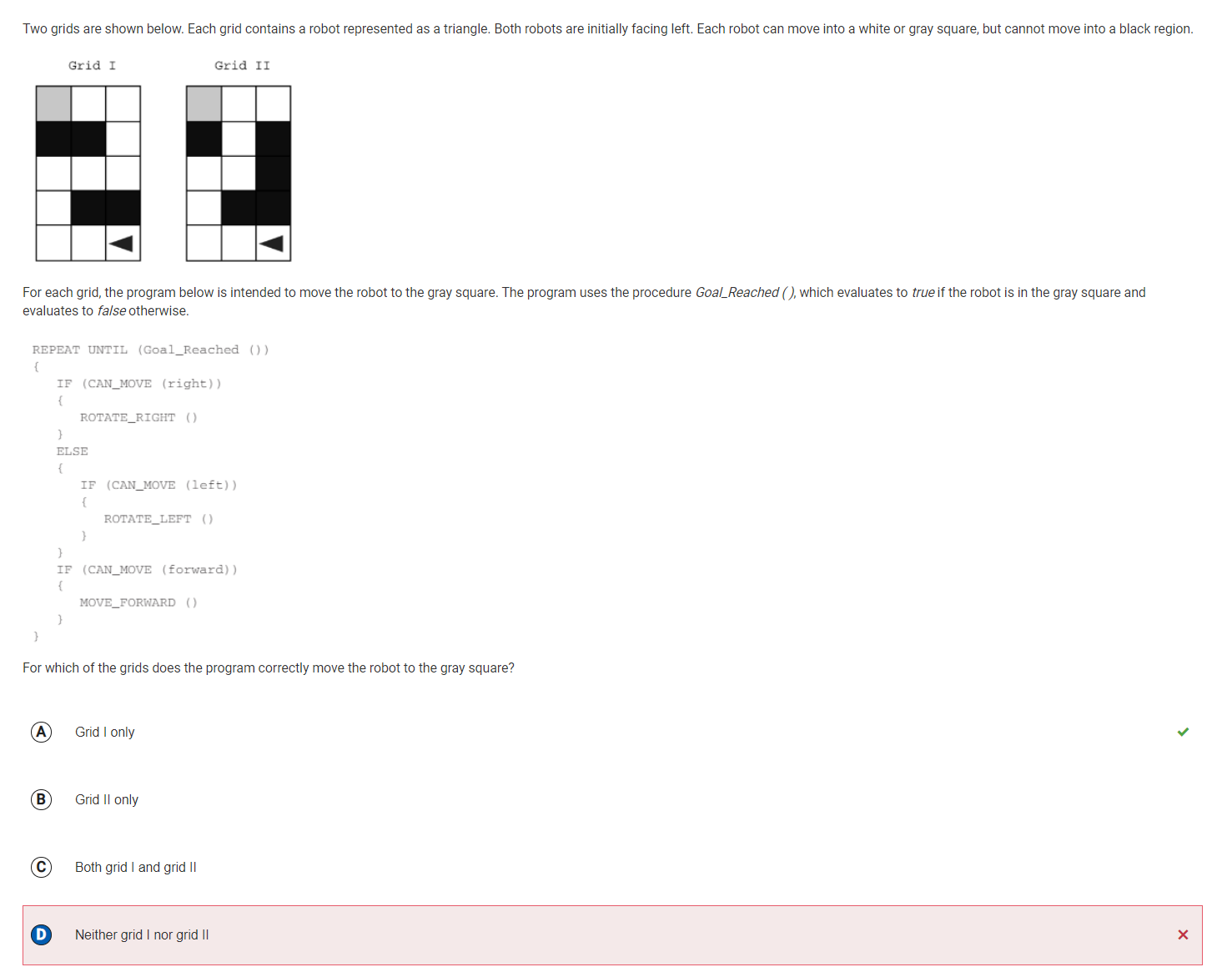
The robot in Grid I proceeds by moving forward along the bottom row until it reaches the end, after which it executes two right turns, moves forward twice, executes two more right turns, and continues moving forward until it reaches the end of the middle row. It then executes two left turns, moves forward twice, executes two more left turns, and proceeds to move forward until it reaches its destination, as indicated by the “Goal_Reached” condition being satisfied.
-
The option is not correct because in Grid II, the robot lands on the middle square of the grid facing right. Although it cannot turn right, it can turn left. It proceeds by moving forward until it reaches the middle square of the top row, at which point it turns left and moves forward to the square in the upper right corner of the grid. However, since the robot cannot move right, left or forward from this square, it becomes stuck in a perpetual loop of the “REPEAT UNTIL” command, as the “Goal_Reached” condition can never be satisfied.
-
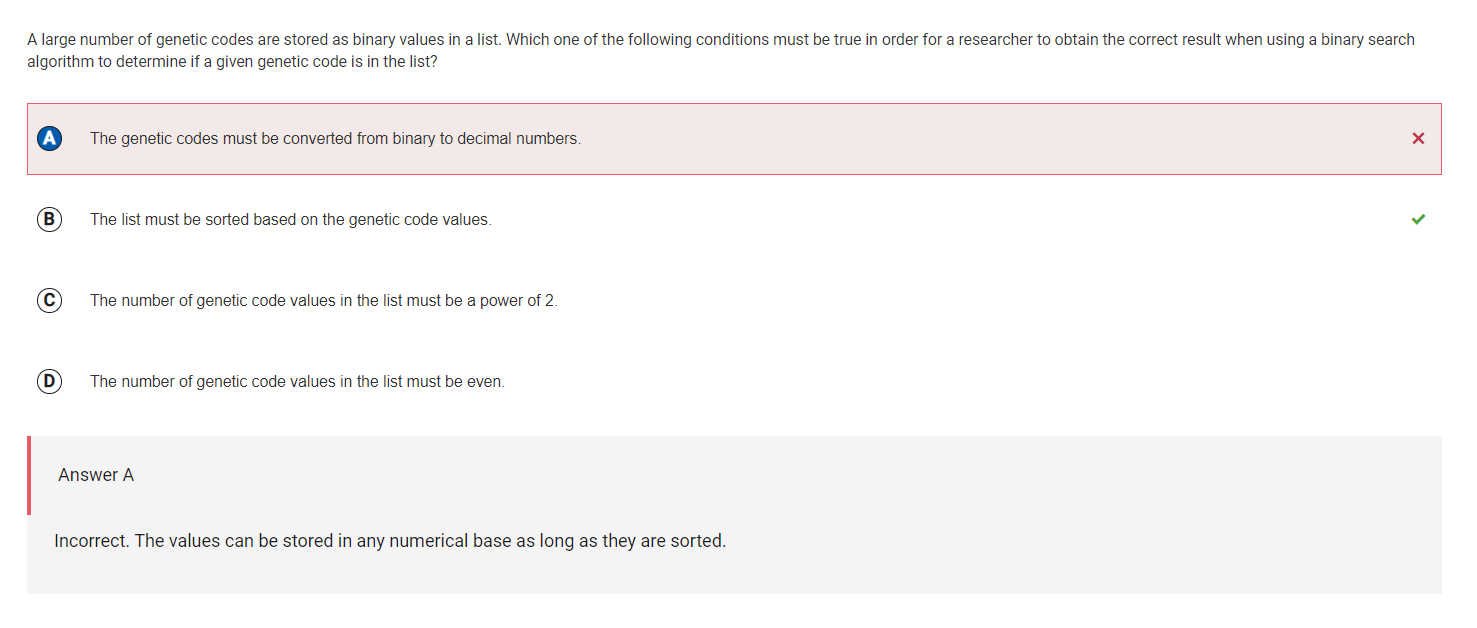
For a binary search to function as intended on a list, it is crucial that the list be sorted in either ascending or descending order. If the list is unsorted, the binary search algorithm will not be able to locate the desired element efficiently, as it relies on the assumption that the middle element of the list is the one being searched for. Therefore, sorting the list before performing a binary search is a prerequisite to ensure its success.
-
This statement is incorrect. Sorting a list of values does not depend on the numerical base used to represent them. The sorting process itself is independent of the numerical base and is only concerned with arranging the values in a specific order. However, when performing operations on the values, such as arithmetic or comparison, it is essential to ensure that the values are represented consistently in the same numerical base.
-
For a binary search algorithm to operate correctly on a list, it is imperative that the list be sorted in either ascending or descending order. The binary search algorithm’s success is based on the premise that it can efficiently locate a desired element in the middle of the sorted list by comparing it to the search value.
-
The accuracy of the binary search operation is not dependent on the numerical base used to store the values being searched. The binary search algorithm is concerned solely with the arrangement of the elements in the list and how they compare to the search value. It does not depend on the representation of the values in any specific numerical base.

- When employing simulations, the extent of their usefulness is determined by the model used in the simulation. The model’s level of complexity and accuracy dictates the level of realism and fidelity of the simulation results. Despite the advantages of having an intricate model, there may be valid reasons for utilizing a simplified model
- One such reason is the ease of implementation. A less complex model may be easier to simulate and analyze, making it more practical and efficient for some applications. Therefore, while a simplified model may not be as realistic, it may still provide useful insights and facilitate understanding of the system being studied.
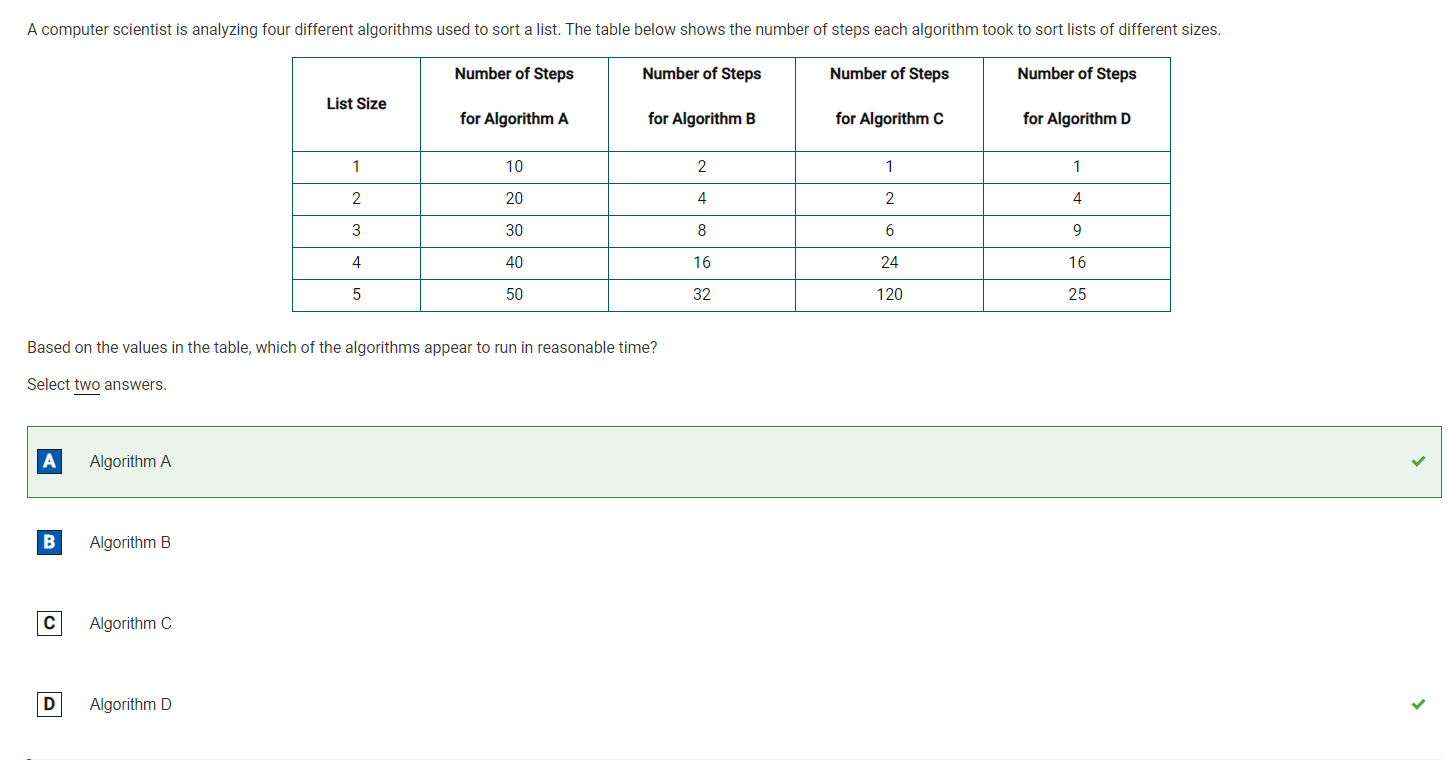
- The number of steps required to sort a list increases linearly as the size of the list increases. Specifically, the number of steps is equal to 10n for a list of size n. This represents a polynomial efficiency, which suggests that the algorithm’s performance remains reasonable as the size of the list increases.