why is it important to know that algorithms that look different can do the same thing and that algorithms that look the same might have different results?(0.15)

  • It is important to know that algorithms that look different can do the same thing so that when working with others and people have various codes it is important to open your mind to understand the code rather than rejecting it because it looks differet. It is also important to know that even code that looks similar can have different purposes so we dont jump to conclusions when evaluating code for the converted conditional to boolean conversion(0.10) total: 0.25
sun = False
raincloud = True

if sun == True:
    print("it is sunny")
else:
    if raincloud == True:
        print("it is cold and rainy")
    else:
        print("not rainy or hot")

it is cold and rainy

sun = False
raincloud = True

sunny = not(raincloud) and sun
if sunny == True:
    print("it is sunny")
if sunny ==False:
    print("it is not sunny")

it is not sunny

3.9.2

Develop your own complex algorithm using a flowchart and natural language, then code it!

If the party has a size 1 the cost is 10 If the party has size 2 the cost is 15 If the party has size 3 then the cost is 20 if the party has size 4 then the cost is 25 print the cost of the party

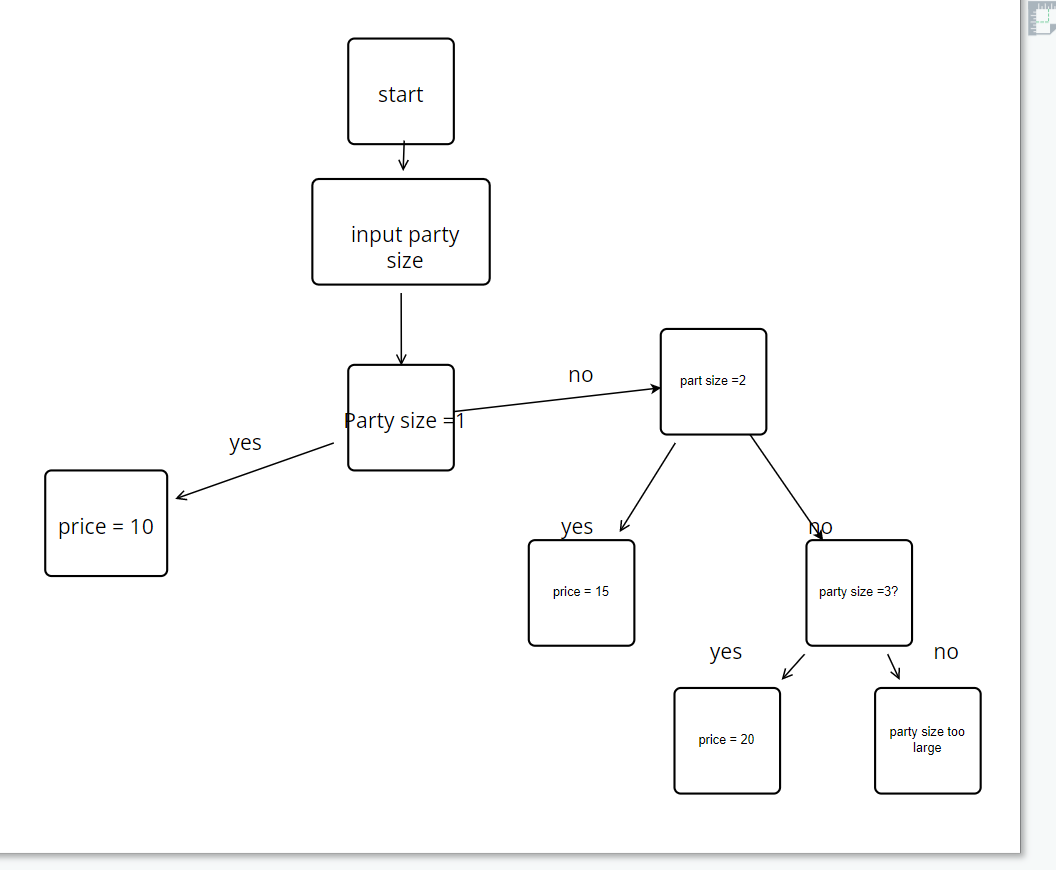
partysize = 4

if partysize ==1:
    print("cost is 10")
elif partysize ==2:
    print("cost is 15")
elif partysize ==3:
    print("cost is 20")
elif partysize ==4:
    print("cost is 25")

cost is 25

3.9.3

Fix the number guessing game

Make a flow chart for the algorithm number guessing game Make a function that gets the user guess Modify the existing search function to give more encouraging feedback

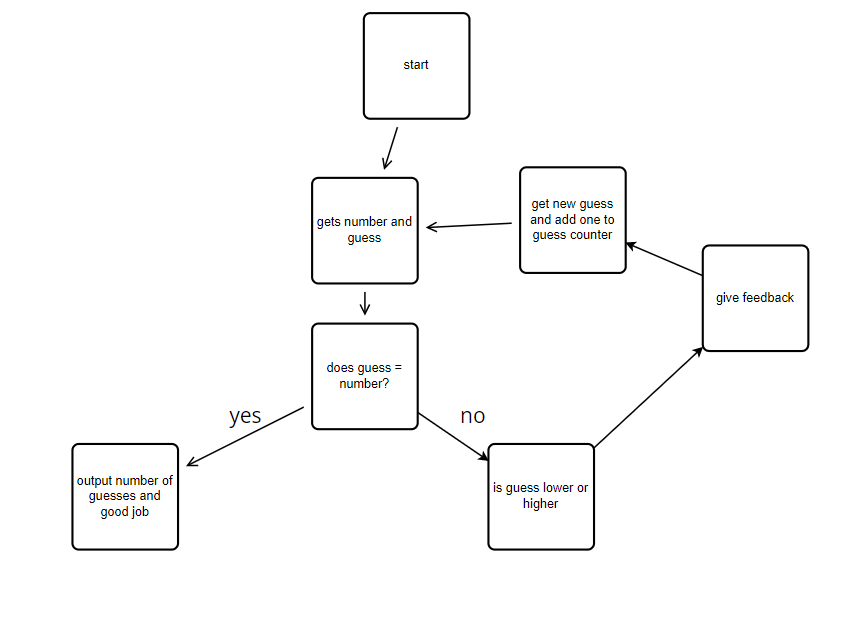
import random

#sets variables for the game
num_guesses = 0
user_guess = 0
upper_bound = 100
lower_bound = 0

#generates a random number
number = random.randint(1,100)

# print(number)     #for testing purposes

print(f"I'm thinking of a number between 1 and 100.")

#Write a function that gets a guess from the user using input()
def guess():
    out = input("What number?")
    return out 

#Change the print statements to give feedback on whether the player guessed too high or too low
def search(number, guess):
    global lower_bound, upper_bound
    if int(guess) < int(number):
        print("below the actual") #change this
        lower_bound = guess
    elif int(guess) > int(number):
        print("above the actual") #change this
        upper_bound = guess
    elif int(guess) == int(number):
        upper_bound = guess
    return lower_bound, upper_bound


while user_guess != number:
    user_guess = guess()
    num_guesses += 1
    print(f"You guessed {user_guess}.")
    lower_bound, upper_bound = search(number, user_guess)
    if int(upper_bound) == int(number):
        break
    else: print(f"Guess a number between {lower_bound} and {upper_bound}.")
print(f"You guessed the number in {num_guesses} guesses!")

I'm thinking of a number between 1 and 100.
You guessed 50.
above the actual
Guess a number between 0 and 50.
You guessed 30.
above the actual
Guess a number between 0 and 30.
You guessed 10.
above the actual
Guess a number between 0 and 10.
You guessed 10.
above the actual
Guess a number between 0 and 10.
You guessed 5.
below the actual
Guess a number between 5 and 10.
You guessed 7.
below the actual
Guess a number between 7 and 10.
You guessed 8.
below the actual
Guess a number between 8 and 10.
You guessed 9.
You guessed the number in 8 guesses!

Hacks: calculate the middle index and create a binary tree for each of these lists 12, 14, 43, 57, 79, 80, 99 92, 43, 74, 66, 30, 12, 1 7, 13, 96, 111, 33, 84, 60

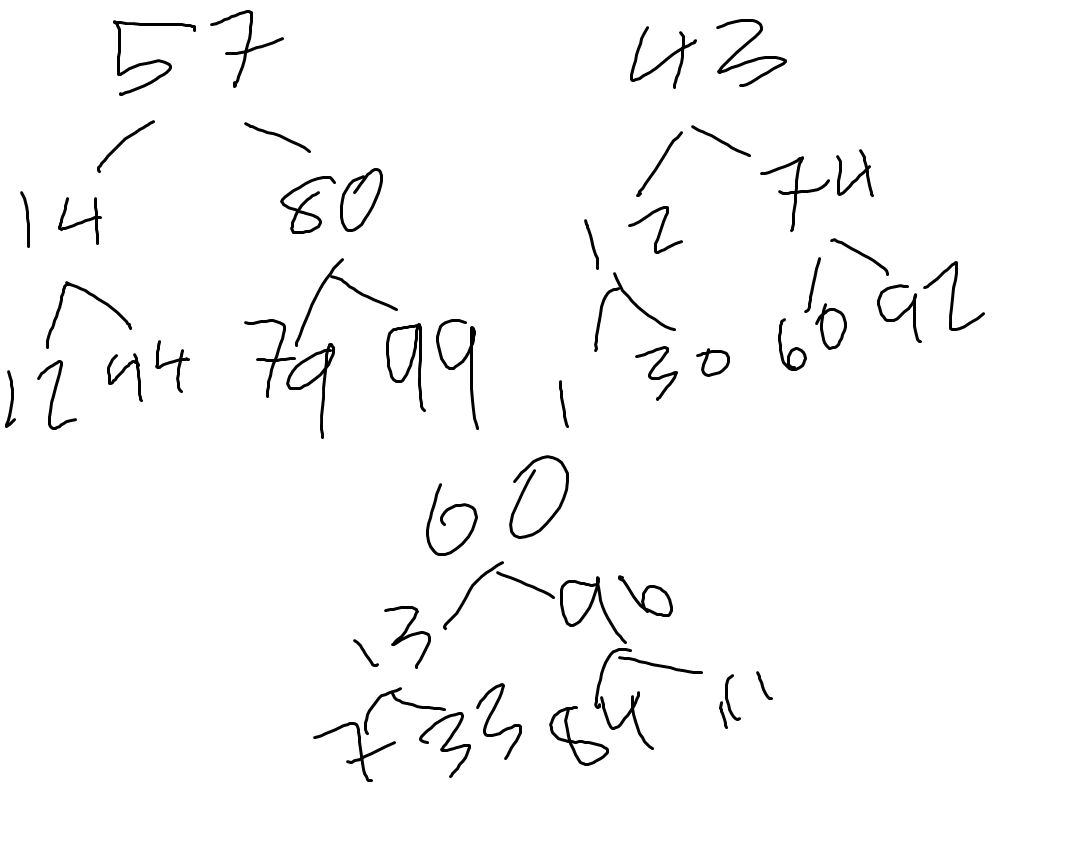
One = [12,14,44,57,79,80,99]
Two = [92,43,74,66,30,12,1]
Three = [7,13,96,111,33,84,60]
Lists = [One, Two, Three]
# loops through the range of the length of lists
for x in range(len(Lists)):
    #sorts the list in order
    Lists[x].sort()
    #takes the middle index 
    middleindex = int(len(Lists[x])/2)
    #outputs
    print("Middle Index of List #",x+1,"is",Lists[x][middleindex])

Middle Index of List # 1 is 57
Middle Index of List # 2 is 43
Middle Index of List # 3 is 60

Using one of the sets of numbers from the question above, what would be the second number looked at in a binary search if the number is more than the middle number? Set 1: 80, Set 2: 74, Set 3: 96

Which of the following lists can NOT a binary search be used in order to find a targeted value?

a. ["amy", "beverly", "christian", "devin"]

b. [-1, 2, 6, 9, 19]

c. [3, 2, 8, 12, 99]

d. ["xylophone", "snowman", "snake", "doorbell", "author"]

c is out of orderso therefore it is c